Die Winkelhalbierende: Unterschied zwischen den Versionen
Main>Bibi-Bot K (Bot: Automatisierte Textersetzung (-{Babel +{Kurzinfo)) |
Main>BigVir |
||
| Zeile 31: | Zeile 31: | ||
Sei ein Winkel α gegeben mit den beiden Halbgerade g und h als Schenkel. <br>Die Symmetrieachse der beiden Halbgeraden g und h heißt '''Winkelhalbierende w''' des Winkels α.}} | Sei ein Winkel α gegeben mit den beiden Halbgerade g und h als Schenkel. <br>Die Symmetrieachse der beiden Halbgeraden g und h heißt '''Winkelhalbierende w''' des Winkels α.}} | ||
|width="30px"| | |width="30px"| | ||
| | | <ggb_applet width="350" height="250" filename="Winkelhalbierende.ggb" showResetIcon="true" /> | ||
|} | |} | ||
Version vom 10. Juni 2008, 18:23 Uhr
| Materialien: 1. 2. |
Die Winkelhalbierende
Arbeitsaufträge:
|  |
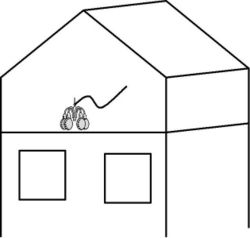
Was ist eine Winkelhalbierende?
Das Seil, an dem die Lampe aufgehängt ist, halbiert den Winkel der beiden Dachflächen. Aufgrund welcher geometrischen Eigenschaft der Winkelhalbierenden konntest Du das Seil konstruieren?
| Vorlage:Kasten blau |  |
Notiere auf Dein Arbeitsblatt:
- Übertrage die Definition der Winkelhalbierenden auf Dein Arbeitsblatt!
Konstruktion der Winkelhalbierenden
Konstruktionsschritte
Arbeitsauftrag:
- Konstruiere mit Zirkel und Lineal die Winkelhalbierende auf Deinem Arbeitsblatt!
- Notiere die besprochenen
 Konstruktionsschritte auf Dein Arbeitsblatt!
Konstruktionsschritte auf Dein Arbeitsblatt!
Konstruktion mit Geogebra
Auch am Computer kann man eine Winkelhalbierende konstruieren!
Arbeitsauftrag:
- Speichere folgende
 GeoGebra-Datei in Deinem Ordner ab und konstruiere mit Geogebra die Winkelhalbierende!
GeoGebra-Datei in Deinem Ordner ab und konstruiere mit Geogebra die Winkelhalbierende! - Orientiere Dich dabei an den Konstruktionsschritten auf dem Arbeitsblatt!
- Speichere die erstellte Konstruktion unter <<Hausdach_DeinName>> im Klassenverzeichnis ab!
Quiz zur Winkelhalbierenden
Sind die Aussagen wahr oder falsch? Beantworte folgende Quizfragen.
Vertiefung bzw. Wiederholung
|
Nachdem nun die Lampe angebracht, |
Aufgaben:
- Öffne die
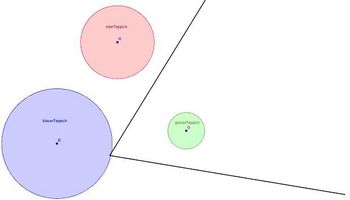
 GeoGebra-Datei und positioniere die drei unterschiedlich großen Teppiche so, dass sie die Wände berühren!
GeoGebra-Datei und positioniere die drei unterschiedlich großen Teppiche so, dass sie die Wände berühren! - Betrachte die Mittelpunkte der Teppiche! Welche besondere Lage haben die Mittelpunkte der drei kreisförmigen Teppiche?
- Konstruiere in der Geogebra-Datei eine Halbgerade, auf der alle Mittelpunkte von runden Teppichen liegen, die beide Wände berühren!
- Speichere die Datei unter "Teppich_<<DeinName>>" im Klassenverzeichnis ab!
Weitere Aufgaben und Hausaufgabe
Schmid A., Weidig I. (Hrsg.): Lambacher Schweizer 7, Mathematik für Gymnasien, Stuttgart 2005:
S. 18 / Nr. 3, 5 und S. 19 / 7
Lernpfad 1. Streich: Die Winkelhalbierende
|
Lernpfad 2. Streich: Die Mittelsenkrechte
|
Lernpfad 3. Streich: Das Lot
|
| Vorlage:Kasten blau |