Benutzer:HWollny/Quadratische Funktionen und ihre Graphen/Parameter d: Unterschied zwischen den Versionen

Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Zeile 38: Zeile 38:
</gallery>
</gallery>
{{Box-spezial
{{Box-spezial
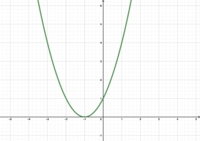
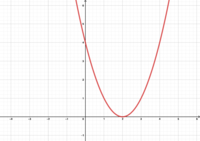
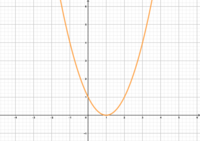
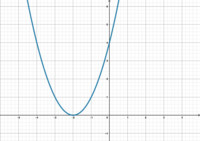
|Titel=  <div align="center"> '''<math>f(x)=(x-2)^2</math>''' <span style="color:#C8C8C8"> hallo </span><math>f(x)=(x-1)^2</math> <span style="color:#C8C8C8"> hallo </span> <math>f(x)=(x+1)^2</math> <span style="color:#C8C8C8"> hallo </span><math>f(x)=(x+2)^2</math> </div>     
|Titel=  <div align="center"> '''<math>f(x)=x^2-2</math>''' <span style="color:#C8C8C8"> hallo </span><math>f(x)=x^2+1</math> <span style="color:#C8C8C8"> hallo </span> <math>f(x)=x^2-4</math> <span style="color:#C8C8C8"> hallo </span><math>f(x)=x^2+3</math> </div>     
|Inhalt=  
|Inhalt=  
|Farbe= Üben         
|Farbe= Üben         
Zeile 45: Zeile 45:
|Hintergrund= #C8C8C8
|Hintergrund= #C8C8C8
}}
}}
*Stellt Vermutungen an, welche Funktionsgleichung zu welchem Graphen gehört.
*Stellt Vermutungen an, welche Funktionsgleichung zu welchem Graphen gehört.
*Überprüft eure Zuordnung anschließend mithilfe von Geogebra.  
*Überprüft eure Zuordnung anschließend mithilfe von Geogebra.
*Beschreibt  die Lage der Graphen der Funktionen <math>f(x)=(x-4)^2</math>und <math>f_5(x)=(x+9)^2</math>, '''ohne''' euch die Graphen anzuschauen.  
*Beschreibt  die Lage der Graphen der Funktionen <math>f(x)=x^2+7</math>und <math>f_5(x)=f(x)=x^2-5</math>, '''ohne''' euch die Graphen anzuschauen.
*Überprüft auch hier eure Vermutungen mithilfe von Geogebra.
*Überprüft auch hier eure Vermutungen mithilfe von Geogebra.


{{Lösung versteckt|
{{Lösung versteckt|
<ggb_applet id="kxb3bzqe" width="700" height="550" />|GeoGebra anzeigen|GeoGebra verbergen}}
<ggb_applet id="kkyrstwv" width="700" height="550" />|GeoGebra anzeigen|GeoGebra verbergen}}






<span class="brainy hdg-spech-bubbles fa-5x"></span> <u>Aufgabe 4</u>'''
<span class="brainy hdg-spech-bubbles fa-5x"></span> <u>Aufgabe 4</u>
Diskutiert den Zusammenhang zwischen dem Parameter d in der Funktionsgleichung  <math>f(x)=(x-d)^2</math> und den dazugehörigen Graphen.
Diskutiert den Zusammenhang zwischen dem Parameter e in der Funktionsgleichung  <math>f(x)=x^2-e</math> und den dazugehörigen Graphen.


*Ihr könnt dafür in dem GeoGebra-Applet verschiedene Zahlen für d einsetzen oder den Schieberegler verschieben.
*Ihr könnt dafür in dem GeoGebra-Applet verschiedene Zahlen für d einsetzen oder den Schieberegler verschieben.
*Überprüft auch hier eure Vermutungen mithilfe von Geogebra.
*Überprüft auch hier eure Vermutungen mithilfe von Geogebra.
{{Lösung versteckt|<ggb_applet id="kxb3bzqe" width="700" height="550" />|GeoGebra anzeigen|GeoGebra verbergen}}
{{Lösung versteckt|<ggb_applet id="kkyrstwv" width="700" height="550" />|GeoGebra anzeigen|GeoGebra verbergen}}
 




Zeile 69: Zeile 69:


<span class="brainy hdg-exclamation fa-2x"></span>
<span class="brainy hdg-exclamation fa-2x"></span>
*WICHTIG: Jeder von euch sollte gleich dazu bereit sein, eure Erkenntnisse den anderen Gruppen vorstellen zu können.
*WICHTIG: Jeder von euch sollte gleich dazu bereit sein, eure Erkenntnisse den anderen Gruppen vorstellen zu können.
*Falls ihr noch Probleme oder Fragen habt, dann tauscht euch in eurer Gruppe darüber aus.
*Falls ihr noch Probleme oder Fragen habt, dann tauscht euch in eurer Gruppe darüber aus.

Version vom 7. August 2022, 12:32 Uhr


Stammgruppe 2

  • D1.png
  • D2.png
  • D3nn.png
  • D4nn.png


Info

Die Funktionen, für die ihr Expertinnen und Experten seid, sind alles quadratische Funktionen der Form .

Der Buchstabe d in der Funktionsgleichung wird Parameter genannt, d.h. wir können für d verschiedene Werte einsetzen und erhalten immer andere Funktionen.

Aufgabe 2
Gebt den Wert von d in den Funktionen an.


Welche Funktionsgleichung gehört zu welchem Graphen?

  • Funktionsgleichung ?

    Funktionsgleichung ?

  • Funktionsgleichung ?

    Funktionsgleichung ?

  • Funktionsgleichung ?

    Funktionsgleichung ?

  • Funktionsgleichung ?

    Funktionsgleichung ?

hallo hallo hallo
  • Stellt Vermutungen an, welche Funktionsgleichung zu welchem Graphen gehört.
  • Überprüft eure Zuordnung anschließend mithilfe von Geogebra.
  • Beschreibt die Lage der Graphen der Funktionen und , ohne euch die Graphen anzuschauen.
  • Überprüft auch hier eure Vermutungen mithilfe von Geogebra.
GeoGebra


Aufgabe 4 Diskutiert den Zusammenhang zwischen dem Parameter e in der Funktionsgleichung und den dazugehörigen Graphen.

  • Ihr könnt dafür in dem GeoGebra-Applet verschiedene Zahlen für d einsetzen oder den Schieberegler verschieben.
  • Überprüft auch hier eure Vermutungen mithilfe von Geogebra.
GeoGebra


Aufgabe 5

Haltet eure Erkenntnisse auf dem Arbeitsblatt zur Vorbereitung für die Expertenrunde fest. Nutzt als Beispiel die Funktion, für die ihr Expertin/Experte seid.

  • WICHTIG: Jeder von euch sollte gleich dazu bereit sein, eure Erkenntnisse den anderen Gruppen vorstellen zu können.
  • Falls ihr noch Probleme oder Fragen habt, dann tauscht euch in eurer Gruppe darüber aus.
Abgerufen von „https://zumunterrichten.idea-sketch.com/index.php?title=Benutzer:HWollny/Quadratische_Funktionen_und_ihre_Graphen/Parameter_d&oldid=129668“