Zentrische Streckung/Eigenschaften der zentrischen Streckung/5.Station: Unterschied zwischen den Versionen

Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Zeile 1: Zeile 1:
<div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;">
{{Navigation verstecken
[[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung|1. Station: Fixelemente]] - [[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/2.Station|2. Station: Geradentreue und Parallelentreue]] - [[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/3.Station|3. Station: Winkeltreue, Längentreue und Flächeninhaltstreue]] - [[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/4.Station|4. Station: Längenverhältnistreue]] - [[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/5.Station|5. Station: Kreistreue]] - [[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/6.Station|6. Station: Zusammenfassung]] - [[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/7.Station|7. Station: Übung]]
|{{Eigenschaften der zentrischen Streckung}}
</div>
|Lernschritte einblenden
<br>
|Lernschritte ausblenden
}}
__NOTOC__


==5. Station: Kreistreue==
==5. Station: Kreistreue==
[[Bild:Porzelt_lobenderDia4.jpg]]
[[Bild:Porzelt_lobenderDia4.jpg]]
<br>
 
<div style="border: 2px solid #ffd700; background-color:#ffffff; padding:7px;">
{{Box|1=Definition Kreistreue|2=
[[Bild:Porzelt_Panto-2.jpg|left]] <br>'''Kreistreue''' liegt vor, wenn das Bild eines Kreises ebenfalls ein Kreis ist.
[[Bild:Porzelt_Panto-2.jpg|right]]
<br>
'''Kreistreue''' liegt vor, wenn das Bild eines Kreises ebenfalls ein Kreis ist.
</div>
|3=Merksatz}}
<br>
 
'''''Mit Hilfe dieses Applets kannst du einen Kreis k zentrisch um den Faktor m = 3 strecken. (Der Streckungsfaktor wurde in'''''<br>
 
'''''diesem Fall mit m bezeichnet, da der Kreis die Abkürzung k besitzt.)'''''<br>
{{Box|1=Wir strecken einen Kreis zentrisch und schauen uns sein Bild an!|2=
'''''Finde heraus, ob die zentrische Streckung kreistreu ist!'''''<br>
 
<div style="border: 2px solid #00CD00; background-color:#ffffff; padding:7px;">
Mit Hilfe dieses Applets kannst du einen Kreis k zentrisch um den Faktor m = 3 strecken. (Der Streckungsfaktor wurde in diesem Fall mit m bezeichnet, da der Kreis die Abkürzung k besitzt.)
{|
 
|<ggb_applet height="350" width="650" showResetIcon="true" filename="Porzelt_Kreistreue.ggb" />||
Finde heraus, ob die zentrische Streckung kreistreu ist!
 
<ggb_applet height="350" width="650" showResetIcon="true" id="a5j36rrm" />
 
<div class="lueckentext-quiz">
<div class="lueckentext-quiz">
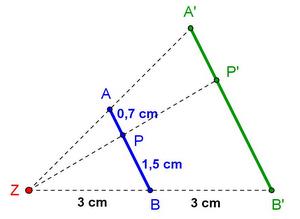
Es gilt: <math>\overline{PM} = r</math> <br>
Es gilt: <math>\overline{PM} = r</math> <br>
Deshalb kann man schreiben: <br>
Deshalb kann man schreiben: <br>
<math>\overline{P'M'} =</math> '''|m|''' <math>\cdot \overline{PM} = r'</math> <br>
<math>\overline{P'M'} =</math> '''\vert m \vert''' <math>\cdot \overline{PM} = r'</math> <br>
Der Bildpunkt P' liegt auf dem '''Kreis k'''' um M' mit Radius <br>
Der Bildpunkt P' liegt auf dem '''Kreis k'''' um M' mit Radius <br>
r' = |m| ∙ '''r'''.
r' = \vert m \vert ∙ '''r'''.
</div>
|}
&nbsp;
</div>
</div>
|3=Arbeitsmethode}}
<br>
<br>
[[Bild:Porzelt_lobenderDia6.jpg]]
[[Bild:Porzelt_lobenderDia6.jpg]]
<br>
<br>


{{Box|1=Kannst du mit den obigen Überlegungen die Frage beantworten?|2=
<div class="multiplechoice-quiz">
<div class="multiplechoice-quiz">
'''Ist die zentrische Streckung kreistreu?'''
'''Ist die zentrische Streckung kreistreu?'''
(Ja) (!Nein)
(Ja) (!Nein)
</div>
</div>
<br>
|3=Frage}}
<div align="left">[[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/6.Station|<math>\Rightarrow</math> Weiter zur 6. Station: Zusammenfassung]]</div>
 
<br>
 
<div align="left">[[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/4.Station|<math>\Leftarrow</math> Zurück zur 4. Station: Längenverhältnistreue]]</div>
{{Fortsetzung|weiter=Längenverhältnistreue|weiterlink=../6.Station}}
 
[[Kategorie:Mathematik]]
[[Kategorie:ZUM2Edutags]]
[[Kategorie:Interaktive Übung]]
[[Kategorie:R-Quiz]]
[[Kategorie:GeoGebra]]

Version vom 6. September 2019, 23:08 Uhr

Eigenschaften der zentrischen Streckung
Porzelt Verhältnistreu.jpg
  1. Fixelemente
  2. Geradentreue und Parallelentreue
  3. Winkeltreue, Längentreue und Flächeninhaltstreue
  4. Längenverhältnistreue
  5. Kreistreue
  6. Zusammenfassung
  7. Übung


5. Station: Kreistreue

Porzelt lobenderDia4.jpg

Definition Kreistreue
Porzelt Panto-2.jpg
Kreistreue liegt vor, wenn das Bild eines Kreises ebenfalls ein Kreis ist.


Wir strecken einen Kreis zentrisch und schauen uns sein Bild an!

Mit Hilfe dieses Applets kannst du einen Kreis k zentrisch um den Faktor m = 3 strecken. (Der Streckungsfaktor wurde in diesem Fall mit m bezeichnet, da der Kreis die Abkürzung k besitzt.)

Finde heraus, ob die zentrische Streckung kreistreu ist!

GeoGebra

Es gilt:
Deshalb kann man schreiben:
\vert m \vert
Der Bildpunkt P' liegt auf dem Kreis k' um M' mit Radius
r' = \vert m \vert ∙ r.


Porzelt lobenderDia6.jpg

Kannst du mit den obigen Überlegungen die Frage beantworten?

Ist die zentrische Streckung kreistreu? (Ja) (!Nein)


Längenverhältnistreue
Abgerufen von „https://zumunterrichten.idea-sketch.com/index.php?title=Zentrische_Streckung/Eigenschaften_der_zentrischen_Streckung/5.Station&oldid=99443“