Trigonometrische Funktionen/Bestimmung der Funktionsgleichung aus dem Graphen: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Main>Silvia Joachim (Avatare auskommentiert) |
Main>Karlo Haberl Keine Bearbeitungszusammenfassung |
||
| Zeile 125: | Zeile 125: | ||
{{Arbeiten|NUMMER=5 - Zusatzaufgabe|ARBEIT= | {{Arbeiten|NUMMER=5 - Zusatzaufgabe|ARBEIT= | ||
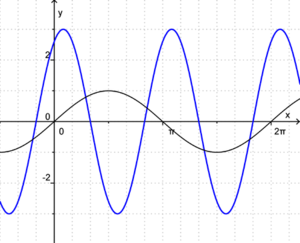
In dem unteren Bild sind die Sinuskurve (rot) und ein Graph einer allgemeinen Sinusfunktion (schwarz) zu sehen.<br> | In dem unteren Bild sind die Sinuskurve (rot) und ein Graph einer allgemeinen Sinusfunktion (schwarz) zu sehen.<br> | ||
[[bild:sin(2x-2).jpg|center]] | |||
# Du kennst die Nullstellen der Sinusfunktion. Wo sind sie?<br> | # Du kennst die Nullstellen der Sinusfunktion. Wo sind sie?<br> | ||
# Stelle in der Zeichnung fest, an welchen Stellen der schwarze Graph Nullstellen besitzt und notiere sie!<br> | # Stelle in der Zeichnung fest, an welchen Stellen der schwarze Graph Nullstellen besitzt und notiere sie!<br> | ||
| Zeile 133: | Zeile 134: | ||
|} | |} | ||
<!-- [[bild:sin(2x-2).jpg|center]] --> | <!-- [[bild:sin(2x-2).jpg|center]] --> | ||
---- | ---- | ||
Version vom 8. Juli 2012, 09:47 Uhr
Einführung - Station 1: Einfluss der Parameter - Station 2: Bestimmung der Funktionsgleichung und mehr - Anwendungen
FAQ
Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.
Station 2: Erfahre, wie du aus dem Graphen einer Funktion deren Term ablesen kannst - und mehr!
Kompetenzen Vorlage:Versteckt
Hefteintrag: Formuliere eine Überschrift und mache dir Notizen zu den Aufgaben!
Bestimmung einer Funktionsgleichung aus dem Graphen
Methoden Vorlage:Versteckt
Jetzt noch was zum Knobeln!!!
Anwendungsbeispiel - Erdbeben
| Vorlage:Arbeiten |
|
Super! Nun hast du es geschafft und das Ende der zweiten Station erreicht. Hefteintrag: Lies dir bitte deinen Hefteintrag durch und überprüfe kurz, ob du wirklich alles Wichtige notiert hast! Beachte, dass in dem Merke-Kasten ein Hefteintrag versteckt ist! Falls du noch etwas üben möchtest, so löse die Zusatzaufgabe! |
Weiter geht es mit Anwendungen