Bruchteile bestimmen

< Mathematik-digital

Lernpfad

Bruchteile bestimmen

 Arbeitsblatt

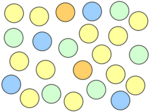
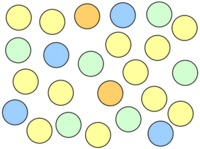
Bestimme den Anteil der gelben, blauen, grünen und orangenen Kringel!

		Hilfe: Grundwissen	Bruchteile : $\frac{1}{2}$; : $\frac{1}{6}$; : $\frac{1}{4}$; : $\frac{1}{12}$

Welcher Anteil der Figur ist gefärbt?

Überlege dir: Wieviele gleich große Teile hat die Figur? Wie viele davon sind gefärbt?

		Hilfe 3 von 6 Teilen sind gefärbt	Bruchteil $\frac{1}{2}$
		Hilfe 2 von 8 Teilen sind gefärbt	Bruchteil $\frac{1}{4}$
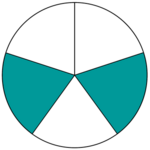
		Hilfe 2 von 5 Teilen sind gefärbt	Bruchteil $\frac{2}{5}$
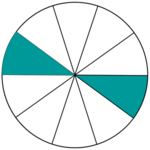
		Hilfe 2 von 10 Teilen sind gefärbt	Bruchteil $\frac{1}{5}$
		Hilfe 3 von 6 Teilen sind gefärbt	Bruchteil $\frac{1}{2}$
		Hilfe 12 von 16 Teilen sind gefärbt	Bruchteil $\frac{3}{4}$

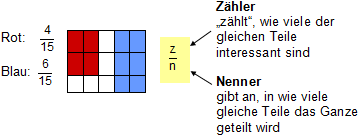
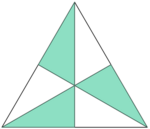
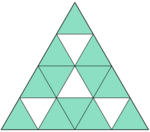
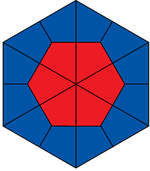
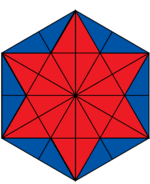
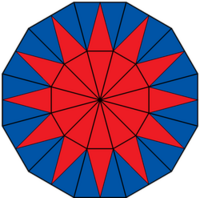
Welcher Bruchteil der Figur ist rot gefärbt?

Überlege dir eine sinnvolle Einteilung der Figur in gleich große Teile! Du findest alle Figuren auf  diesem Blatt zum Download.

		Hilfe	Bruchteil $\frac{1}{3}$
		Hilfe	Bruchteil $\frac{2}{3}$
		Hilfe	Bruchteil $\frac{1}{4}$
schwer		Hilfe	Bruchteil $\frac{1}{2}$

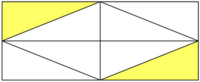
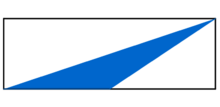
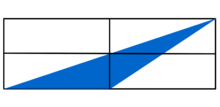
Welcher Bruchteil der Figur ist blau gefärbt?

		Hilfe	Bruchteil $\frac{1}{4}$

Hinweis zu alternativer Lösung

Wie verändert sich die Fläche des blauen Dreiecks, wenn die obere Ecke nach links verschoben wird?

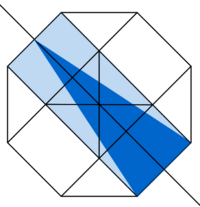
schwer		Hilfe 1	Hilfe 2	Bruchteil $\frac{1}{4}$

Hinweis zu alternativer Lösung

Wie verändert sich die Fläche des blauen Dreiecks, wenn die Höhe halbiert wird? Lässt sich zu solch einem Dreieck die Fläche durch Symmetrieüberlegungen finden?

Komplette Lösung zum Arbeitsblatt

Zurück zum Grundwissen Brüche

Vorlage:Mitgewirkt<metakeywords>ZUM2Edutags,ZUM-Wiki,Bruchteile bestimmen,Mathematik-digital, Lernpfad, Bruch, Brüche, Bruchrechnung, interaktive Übungen, Mathematik, 6. Klasse, Sekundarstufe 1</metakeywords>