Benutzer:HWollny/Lineare Funktionen: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
(Die Seite wurde neu angelegt: „{{Box-spezial |Titel= Info |Inhalt= Die Funktionen, für die ihr Expertinnen und Experten seid, sind alles lineare Funktionen der Form '''''<math>f(x)=m\cdot…“) Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 1: | Zeile 1: | ||
<gallery widths="200" heights="200" style="text-align:center"> | |||
Datei:EinstiegsbildlF.png</gallery> | |||
{{Box-spezial | {{Box-spezial | ||
|Titel= Info | |Titel= Info | ||
| Zeile 8: | Zeile 10: | ||
|Hintergrund= #c4e3e8 | |Hintergrund= #c4e3e8 | ||
}} | }} | ||
<span class="brainy hdg-spech-bubbles fa-5x"></span> <u>Was passiert mit dem Graphen der linearen Funktion, wenn '''m''' sich verändert? </u> | |||
# Verändert in der GeoGebra-Datei mit Hilfe des Schiebereglers den Wert des Parameters '''m''' und beobachtet, wie sich '''der Graph''' und die '''Funktionsgleichung''' verändern. | |||
# Haltet eure Beobachtungen in der Tabelle fest und beschreibt die Veränderungen mit Hilfe von unterschiedlichen Beispielen, indem du jeweils auf den Verlauf des Graphen eingehst. | |||
z.B.: <math>m = 2</math>: Der Graph der Funktion ... | |||
# Haltet in der Sprechblase auf dem AB die '''allgemeine Bedeutung''' des Parameters '''m''' für den Graphen linearer Funktionen fest. | |||
Version vom 24. November 2022, 14:17 Uhr
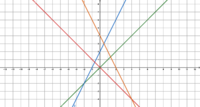
Was passiert mit dem Graphen der linearen Funktion, wenn m sich verändert?
- Verändert in der GeoGebra-Datei mit Hilfe des Schiebereglers den Wert des Parameters m und beobachtet, wie sich der Graph und die Funktionsgleichung verändern.
- Haltet eure Beobachtungen in der Tabelle fest und beschreibt die Veränderungen mit Hilfe von unterschiedlichen Beispielen, indem du jeweils auf den Verlauf des Graphen eingehst.
z.B.: : Der Graph der Funktion ...
- Haltet in der Sprechblase auf dem AB die allgemeine Bedeutung des Parameters m für den Graphen linearer Funktionen fest.