Benutzer:HWollny/Quadratische Funktionen und ihre Graphen/Parameter d
|
|
| Zeile 54: |
Zeile 54: |
|
| |
|
|
| |
|
|
| |
|
| |
|
| |
| <span class="brainy hdg-spech-bubbles fa-5x"></span>
| |
| {{Box-spezial | | {{Box-spezial |
| |Titel= '''<u>Aufgabe 4</u>''' | | |Titel= <span class="brainy hdg-spech-bubbles fa-5x"></span> '''<u>Aufgabe 4</u>''' |
| |Inhalt= | | |Inhalt= |
| Diskutiert den Zusammenhang zwischen dem Parameter d in der Funktionsgleichung <math>f(x)=(x-d)^2</math> und den dazugehörigen Graphen. | | Diskutiert den Zusammenhang zwischen dem Parameter d in der Funktionsgleichung <math>f(x)=(x-d)^2</math> und den dazugehörigen Graphen. |
| Zeile 72: |
Zeile 68: |
| |Hintergrund= #C8C8C8 | | |Hintergrund= #C8C8C8 |
| }} | | }} |
|
| |
|
| |
|
|
| |
|
Version vom 7. August 2022, 12:00 Uhr
Stammgruppe 2
Info
Die Funktionen, für die ihr Expertinnen und Experten seid, sind alles quadratische Funktionen der Form  .
.
Der Buchstabe
d in der Funktionsgleichung wird
Parameter genannt, d.h. wir können für d verschiedene Werte einsetzen und erhalten immer andere Funktionen.
Aufgabe 2
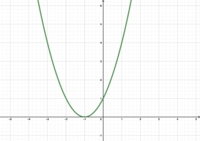
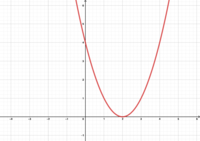
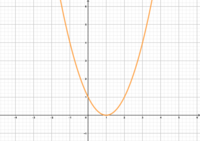
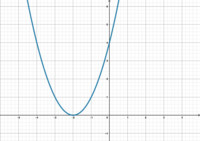
Gebt den Wert von d in den Funktionen an.
Welche Funktionsgleichung gehört zu welchem Graphen?
f(x)=(x-2)2 hallo g(x)=(x+2)2 hallo h(x)=(x+1)2 hallo k(x)=(x-1)2
- Stellt Vermutungen an, welche Funktionsgleichung zu welchem Graphen gehört.
- Überprüft eure Zuordnung anschließend mithilfe von Geogebra.
- Beschreibt die Lage der Graphen der Funktionen
 und
und  , ohne euch die Graphen anzuschauen.
, ohne euch die Graphen anzuschauen.
- Überprüft auch hier eure Vermutungen mithilfe von Geogebra.
Aufgabe 4
Diskutiert den Zusammenhang zwischen dem Parameter d in der Funktionsgleichung  und den dazugehörigen Graphen.
und den dazugehörigen Graphen.
- Ihr könnt dafür in dem GeoGebra-Applet verschiedene Zahlen für d einsetzen oder den Schieberegler verschieben.
- Überprüft auch hier eure Vermutungen mithilfe von Geogebra.
Aufgabe 5
Haltet eure Erkenntnisse auf dem Arbeitsblatt zur Vorbereitung für die Expertenrunde fest. Nutzt als Beispiel die Funktion, für die ihr Expertin/Experte seid.
- WICHTIG: Jeder von euch sollte gleich dazu bereit sein, eure Erkenntnisse den anderen Gruppen vorstellen zu können.
- Falls ihr noch Probleme oder Fragen habt, dann tauscht euch in eurer Gruppe darüber aus.