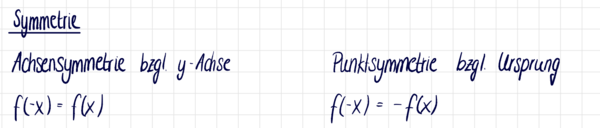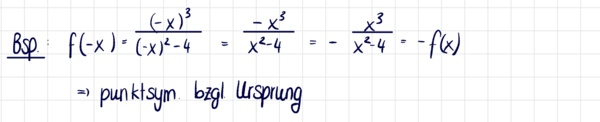Symmetrieuntersuchung: Unterschied zwischen den Versionen

Aktuelle Version vom 12. Dezember 2022, 09:42 Uhr

Es ist sinnvoll die Symmetrie früh zu untersuchen, da man so von den Erkenntnissen auf einer Seite der y-Achse auf die andere schließen kann.

Untersuche die Beispielfunktion $f(x)=\frac{x^3}{x^2-4}$ auf Symmetrie.

@@ Zeile 1: / Zeile 1: @@
-Es ist sinnvoll die Symmetrie früh zu untersuchen, da so von den Erkenntnissen auf einer Seite der y-Achse auf die andere schließen kann.
+Es ist sinnvoll die Symmetrie früh zu untersuchen, da man so von den Erkenntnissen auf einer Seite der y-Achse auf die andere schließen kann.
-[[[[Teil 1]]| zurück]]
+<br /><span class="brainy hdg-pencil  fa-3x" "></span>
+[[Datei:Symmetrie Erklärung.png|alternativtext=|ohne|mini|600x600px]]
+<p> </p>
+<p> </p>
-{{Fortsetzung|vorher=zurück|vorherlink=Definitionsbereich|weiter=Symmetrie|weiterlink=Schnittpunkt mit den Achsen}}
+<span class="brainy hdg-ruler-pencil  fa-3x" "></span> Untersuche die Beispielfunktion <math>f(x)=\frac{x^3}{x^2-4}</math> auf Symmetrie.
-{{Fortsetzung|vorher=zurück zu Teil 1|vorherlink=Teil 1}}
+{{Lösung versteckt|[[Datei:Symmetrie FKt.png|alternativtext=|ohne|mini|600x600px]]|Lösung anzeigen|Lösung verbergen}}
+<span class="brainy hdg-screen01  fa-3x" "></span>
+{{LearningApp
+| app = 21415233
+| height = 350px
+}}
+<br />
+{{Fortsetzung|vorher=zurück|vorherlink=Definitionsmenge|weiter=Schnittpunkte mit den Achsen|weiterlink=Schnittpunkt mit den Achsen}}
+{{Fortsetzung|vorher=zurück zur Übersicht|vorherlink=Funktionsuntersuchung}}