Sinus- und Kosinusfunktion/3. Allgemeine Sinusfunktion: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Main>Florian Ferstl Keine Bearbeitungszusammenfassung |
Main>Karl Kirst (Merksatz > Merke) |
||
| Zeile 41: | Zeile 41: | ||
Schreibe folgenden Hefteintrag in dein Schulheft! | Schreibe folgenden Hefteintrag in dein Schulheft! | ||
''' | ''' | ||
{{ | {{Merke|1= | ||
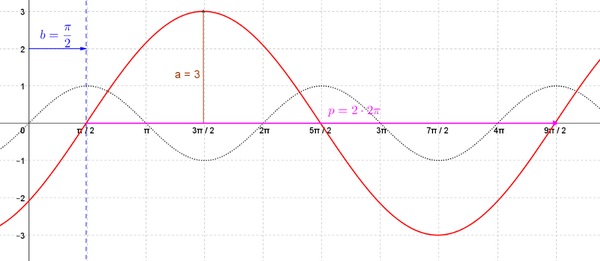
Die allgemeine Sinuskurve <math> y = a\cdot sin(b\cdot(x-c)+d </math> geht so aus der normalen Sinuskurve <math> y=sin(x)</math> hervor: <br> | Die allgemeine Sinuskurve <math> y = a\cdot sin(b\cdot(x-c)+d </math> geht so aus der normalen Sinuskurve <math> y=sin(x)</math> hervor: <br> | ||
* Die Amplitude ist der Betrag von a . Die y-Werte liegen also zwischen -a und a. Bei negativem a wird noch an der x-Achse gespiegelt. | * Die Amplitude ist der Betrag von a . Die y-Werte liegen also zwischen -a und a. Bei negativem a wird noch an der x-Achse gespiegelt. | ||
Version vom 11. März 2018, 11:06 Uhr
Vorlage:Lernpfad Sinus und Kosinusfunktion
Station 3: Die allgemeine Sinusfunktion
Sinusfunktionen und Kosinusfunktionen schauen nicht immer gleich aus. z.B.Allgemein:
In dieser Station findest du heraus, wie sich die vier Parameter a, b, c und d auf den Verlauf des Graphen auswirken. Viel Spass!
Was ist was?
Halte deine Erkenntniss nun fest: Vorlage:Aufgaben-M
| <popup name = "Lösung 3a">
a: verändert die Amplitude, also Strecken bzw. Stauchen in y-Richtung
Merke Die allgemeine Sinuskurve geht so aus der normalen Sinuskurve hervor:
Ok, jetzt schauen wir uns die drei Parameter noch etwas genauer an. Have fun...!
| ||