Sinus- und Kosinusfunktion/2.2 Kosinusfunktion: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Main>Florian Ferstl |
Main>Florian Ferstl Keine Bearbeitungszusammenfassung |
||
| Zeile 2: | Zeile 2: | ||
<div style=" width: | <div style=" width: 95%; border: 2px solid #c6d745; background-color:#c6d745; padding:7px;font-size:1px; height:1px; border-bottom:1px solid #c6d745;"></div> | ||
<div style=" width: | <div style=" width: 95%; border: 2px solid #c6d745; background-color:#ffffff; align:center; padding:7px;"> | ||
==Station 2: Sinusfunktion und Kosinusfunktion== | ==Station 2: Sinusfunktion und Kosinusfunktion== | ||
| Zeile 9: | Zeile 9: | ||
{| | {| | ||
==2.2 Kosinusfunktion== | |||
{{Auftrag| | |||
Versuche dir nochmal klarzumachen, wie die Kosinus-Funktion aus dem Einheitskreis entsteht. Dazu übertragen wir die Bogenlänge b auf die x-Achse (s. grüne Linie). <br> | Versuche dir nochmal klarzumachen, wie die Kosinus-Funktion aus dem Einheitskreis entsteht. Dazu übertragen wir die Bogenlänge b auf die x-Achse (s. grüne Linie). <br> | ||
Nun tragen wir die Kosinuswerte, die zum eingestellten Winkel gehören, als y-Werte ein. | Nun tragen wir die Kosinuswerte, die zum eingestellten Winkel gehören, als y-Werte ein. | ||
<br>Durch Klick auf die Checkbox „Kosinuswert als Punkt einer Funktion“ kannst du die einzelnen Funktionswerte anzeigen lassen. Schalte die Spur des Punktes A ein, um die Funktion zu zeichnen. | <br>Durch Klick auf die Checkbox „Kosinuswert als Punkt einer Funktion“ kannst du die einzelnen Funktionswerte anzeigen lassen. Schalte die Spur des Punktes A ein, um die Funktion zu zeichnen. | ||
<iframe scrolling="no" title="Kosinusfunktion am Einheitskreis" src="https://www.geogebra.org/material/iframe/id/AtX3XWby/width/1648/height/670/border/888888/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/true/ctl/false" width=" | <iframe scrolling="no" title="Kosinusfunktion am Einheitskreis" src="https://www.geogebra.org/material/iframe/id/AtX3XWby/width/1648/height/670/border/888888/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/true/ctl/false" width="920px" height="365px" style="border:0px;"> </iframe> | ||
}} | |||
<br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br> | |||
Bearbeite den zugehörigen Auftrag auf dem Arbeitsblatt. | Halte deine Erkenntnisse nun schriftlich fest: | ||
{{Aufgaben-M|2.2 Sinusfunktion|Bearbeite den zugehörigen Auftrag auf dem Arbeitsblatt.}} | |||
<br> | <br> | ||
{{Frage| | |||
Überlege: Was könnte das bedeuten? | Überlege: Was könnte das bedeuten? | ||
<math> cos(-\frac{\pi}{2}) </math> oder <math> cos(410^\circ) </math> | <math> cos(-\frac{\pi}{2}) </math> oder <math> cos(410^\circ) </math> | ||
Schreibe die Lösung (gerne auch in eigenen Worten) in dein Schulheft. | Schreibe die Lösung (gerne auch in eigenen Worten) in dein Schulheft. | ||
}} | |||
<br> | <br> | ||
{| | {| | ||
|<popup name = "Lösung negativer Winkel"> | |<popup name = "Lösung negativer Winkel"> | ||
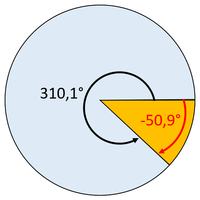
Ein negativer Winkel bedeutet, dass man den Winkel nicht '''im ''' Uhrzeigersinn anträgt, sondern im Gegenuhrzeigersinn. | Ein negativer Winkel bedeutet, dass man den Winkel nicht '''im ''' Uhrzeigersinn anträgt, sondern im Gegenuhrzeigersinn. | ||
| Zeile 45: | Zeile 49: | ||
<br> | <br> | ||
<br> | <br> | ||
''' | Teste, ob du alles verstanden hast! | ||
{{Übung|'''Kosinusfunktion verstanden?''' | |||
<br> | |||
<iframe src="https://learningapps.org/watch?v=p12tazmca17" style="border:0px;width:80%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="https://learningapps.org/watch?v=p12tazmca17" style="border:0px;width:80%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
}} | |||
---- | ---- | ||
Version vom 13. November 2017, 16:43 Uhr
Vorlage:Lernpfad Sinus und Kosinusfunktion
Station 2: Sinusfunktion und Kosinusfunktion
2.2 Kosinusfunktion
Halte deine Erkenntnisse nun schriftlich fest:
Vorlage:Aufgaben-M
Frage
Überlege: Was könnte das bedeuten?
oder
Schreibe die Lösung (gerne auch in eigenen Worten) in dein Schulheft.
| <popup name = "Lösung negativer Winkel">
Ein negativer Winkel bedeutet, dass man den Winkel nicht im Uhrzeigersinn anträgt, sondern im Gegenuhrzeigersinn. ok? </popup>
|
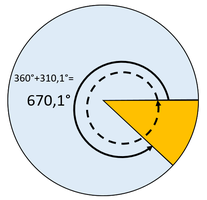
<popup name = "Lösung große Winkel">
Ein Winkel, der größer als 360° ist entsteht, wenn man quasi mehr als eine Umdrehung macht. Also 1,5 Umdrehungen wären dann 360°+180° = 440° oder ok? </popup> |
Teste, ob du alles verstanden hast!
Übung
Kosinusfunktion verstanden?
Erste Wiederholung ist geschafft. War nicht so schwer. Weiter gehts! :)
| Hier geht es weiter... |