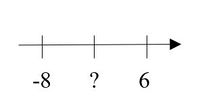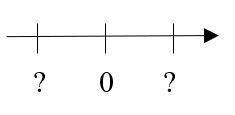Einführung in die Negativen Zahlen/Erweiterung der Zahlengeraden: Unterschied zwischen den Versionen
Main>Anto23 Keine Bearbeitungszusammenfassung |
Main>Anto23 Keine Bearbeitungszusammenfassung |
||
| Zeile 14: | Zeile 14: | ||
|} | |} | ||
{{Aufgabe|{{protokollieren}} | {{Aufgabe|{{protokollieren}} | ||
Betrachtet das Merkekästchen. | Betrachtet das Merkekästchen. Ordnet den Satzanfängen das richtige Satzende zu und übernehmt die Sätze dann auf euer Protokoll.}} | ||
{|width=100% | |||
|- | |||
|width=50%| | |||
{{Merke| | {{Merke| | ||
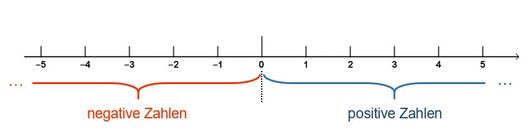
Wir erweitern unseren bekannten Zahlenstrahl zu einer Zahlengeraden.<br> | Wir erweitern unseren bekannten Zahlenstrahl zu einer Zahlengeraden.<br> | ||
[[Datei:Zahlengerade2.JPG|600px|links]]}} | [[Datei:Zahlengerade2.JPG|600px|links]]}} | ||
< | |width=50%| | ||
<div class="lueckentext-quiz"> | |||
{| | |||
|- | |||
| Die negativen Zahlen liegen || '''links von der Null.''' | |||
|- | |||
| Die positiven Zahlen liegen || '''rechts von der Null.''' | |||
|- | |||
| Die Null liegt|| '''in der Mitte.''' | |||
|} | |||
</div> | |||
|} | |||
<br><br> | <br><br> | ||
{{Übung|Bearbeitet die folgenden Aufgaben.}} | {{Übung|Bearbeitet die folgenden Aufgaben.}} | ||
Version vom 17. April 2018, 10:24 Uhr
|
Frage
Was ist der Unterschied zwischen der 4 unter der Null und der 4 über der Null?
|
|
|
|
|
|
1. Findet zu jeder Situation eine passende ganze Zahl. Ordnet die Situation an die richtige Stelle auf der Zahlengeraden.
|
2. Welche Zahl liegt in der Mitte zwischen -8 und 6? Benutzt die Zahlengerade, um die Aufgabe zu lösen. Beschreibt auf dem Protokoll, wie ihr die Aufgabe gelöst habt.
-1 liegt in der Mitte zwischen -8 und 6.
|
3. Von den beiden folgenden Aufgaben könnt ihr eine auswählen. Die linke Aufgabe ist etwas leichter als die rechte Aufgabe. Für beide Aufgaben könnt ihr die Zahlengerade benutzen.
|
Welche Zahl liegt genau in der Mitte der angegebenen Zahlen?[2] |
Entgegengesetzte Zahlen und Betrag
Welche Zahlen könnt ihr für die Fragezeichen einsetzen? Löst und begründet eure Antwort auf dem Protokoll.
<popup name="Lösungsvorschlag"> Man kann für die Fragezeichen alle Zahlen einsetzen, die sich nur durch das Vorzeichen unterscheiden, also z.B. -3 & 3, -18 & 18, -5 & 5,… , da diese Zahlenpaare denselben Abstand zur 0 haben. </popup>
- Lest euch das Merkekästchen gut durch.
- Löst die Aufgaben in den Learning Apps.
- Notiert auf eurem Protokoll drei Beispiele zu entgegengesetzten Zahlen und zwei Beispiele zum Betrag. Ihr könnt Beispiele aus den Aufgaben nehmen.
- Zwei Zahlen, die ein entgegengesetztes Vorzeichen, aber zur Null denselben Abstand haben, heißen entgegengesetzte Zahlen.
- Der Abstand einer Zahl zur 0 heißt Betrag und wird mit Betragsstrichen gekennzeichnet, z.B. |-4| = 4; |+4| = 4.
Weitere Erklärungen zum Betrag
Der Betrag gibt den Abstand von einer Zahl zur 0 an. Sowohl von der -9 als auch von der 9 muss man 9 Schritte bis zur 0 gehen. Deswegen haben -9 und 9 denselben Abstand, also auch denselben Betrag. Der Betrag ist immer positiv, hat also immer ein "+" als Vorzeichen, weil man ja nicht z.B. -9 Schritte gehen kann. Der Betrag der 0 ist 0, da man ja keine Schritte mehr laufen muss, um zur 0 zu gelangen.
|
Übung zu den entgegengesetzten Zahlen |
Übung zum Betrag |
|
|
|