Benutzer:HWollny/Quadratische Funktionen und ihre Graphen/Experten1: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 16: | Zeile 16: | ||
# Überprüft eure Beschreibung mithilfe von GeoGebra. | # Überprüft eure Beschreibung mithilfe von GeoGebra. | ||
<ggb_applet id="bbfrtrzv" width="700" height="550" /> | |||
'''<u> Verallgemeinerung </u>''' | '''<u> Verallgemeinerung </u>''' | ||
| Zeile 25: | Zeile 26: | ||
Datei:Verallgemeinerung.png| | Datei:Verallgemeinerung.png| | ||
</gallery> | </gallery> | ||
Die Normalparabel soll um 2 Einheiten nach links und um 8 Einheiten nach unten verschoben werden. Wie lautet die Funktionsgleichung? Überprüft anschließend mit GeoGebra. | |||
Die Normalparabel soll um 4 Einheiten nach rechts und um 2,5 Einheiten nach oben verschoben werden. Wie lautet die Funktionsgleichung? Überprüft anschließend mit GeoGebra. | |||
Version vom 8. August 2022, 21:10 Uhr
Expertengruppe 1
Austausch
- Stellt euch gegenseitig vor, welche Informationen ihr über die Lage einer Parabel anhand der Funktionsgleichung ablesen könnt. Nutzt dazu euer Vorbereitungsblatt und das Bild, mit eurem Funktionsgraphen
- Beschreibt anschließend in den Sprechblasen auf dem Arbeitsblatt, wie die Funktion im Vergleich zur Normalparabel verläuft.
- Überprüft eure Beschreibung mithilfe von GeoGebra.

Verallgemeinerung
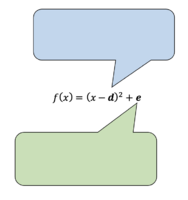
Erklärt in den Sprechblasen auf dem Arbeitsblatt allgemein, welchen Einfluss die Parameter d und e auf den Graphen einer Normalparabel haben.
Die Normalparabel soll um 2 Einheiten nach links und um 8 Einheiten nach unten verschoben werden. Wie lautet die Funktionsgleichung? Überprüft anschließend mit GeoGebra.
Die Normalparabel soll um 4 Einheiten nach rechts und um 2,5 Einheiten nach oben verschoben werden. Wie lautet die Funktionsgleichung? Überprüft anschließend mit GeoGebra.