Benutzer:Verena.eisenkoeck/Lernpfad Prozentrechnung/Graphische Darstellung: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (16 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 24: | Zeile 24: | ||
'''Beispiel:'''[[Datei:Hundertertafel.png|mini|alternativtext=|zentriert]] | '''Beispiel:'''[[Datei:Hundertertafel.png|mini|alternativtext=|zentriert]] | ||
<div class="lueckentext-quiz">Im Hunderterfeld sind ''' | <div class="lueckentext-quiz">Im Hunderterfeld sind '''42()''' Kästchen eingefärbt, das entspricht '''42()'''% des Grundwerts. </div> | ||
<br> | <br> | ||
{{Box|Aufgabe|Nimm dir ein Blatt Papier und einen Stift. Übertrage die folgenden Prozentangaben auf dein Blatt und zeichne dazu die passenden Hunderterfelder. | {{Box|Aufgabe|Nimm dir ein Blatt Papier und einen Stift. Übertrage die folgenden Prozentangaben auf dein Blatt und zeichne dazu die passenden Hunderterfelder. | ||
| Zeile 55: | Zeile 55: | ||
===3. Prozentkreis=== | ===3. Prozentkreis=== | ||
Beim Prozentkreis wird das Ganze als eine volle Kreisfläche dargestellt. | Beim '''Prozentkreis''' wird das '''Ganze''' als eine '''volle Kreisfläche''' dargestellt. | ||
100% entsprechen also 360°. | '''100% entsprechen also 360°'''. | ||
Für einen kleineren Prozentsatz zeichnet man einen Kreissektor. Dafür muss der Winkel entsprechend dem dazugehörigen Prozentsatz berechnet werden. Wenn 100% also 360° entsprechen, dann entspricht 1% genau 3,6°. | Für einen kleineren Prozentsatz zeichnet man einen '''Kreissektor'''. Dafür muss der '''Winkel''' entsprechend dem dazugehörigen Prozentsatz berechnet werden. Wenn 100% also 360° entsprechen, dann entspricht '''1% genau 3,6°'''. | ||
<br />{{Box|Aufgabe|Ergänze mit dem GeoGebra Applet die nebenstehende Tabelle:|Arbeitsmethode | <br />{{Box|Aufgabe|Ergänze mit dem GeoGebra-Applet die nebenstehende Tabelle:|Arbeitsmethode | ||
}} | }} | ||
<br> | |||
{| class="wikitable" | {| class="wikitable" | ||
!'''Prozentsatz''' | !'''Prozentsatz''' | ||
!''' | !'''Winkel des Kreissektors''' | ||
! rowspan="7" |<ggb_applet id="bqgbwzd3" width="400" height="510">GeoGebra-Applet: verändere die Prozentangabe um den entsprechenden Winkel zu erhalten!</ggb_applet> | |||
|- | |- | ||
|5% | |5% | ||
| Zeile 88: | Zeile 89: | ||
<br /> | <br /> | ||
Aktuelle Version vom 2. April 2021, 08:36 Uhr
Graphische Darstellung von Prozentangaben
Wie kann man nun Prozentangaben graphisch darstellen?
Wir betrachten die folgenden Möglichkeiten:
- Hunderterfeld
- Prozentstreifen
- Prozentkreis
1. Hunderterfeld
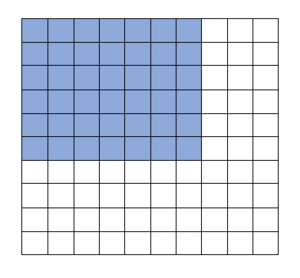
Das Hunderterfeld ist ein Feld mit 100 Kästchen (10x10). Das gesamte Feld entspricht 100%. Ein Kästchen entspricht daher 1%.
Du kannst den Prozentsatz an den eingefärbten Kästchen ablesen.
Beispiel:
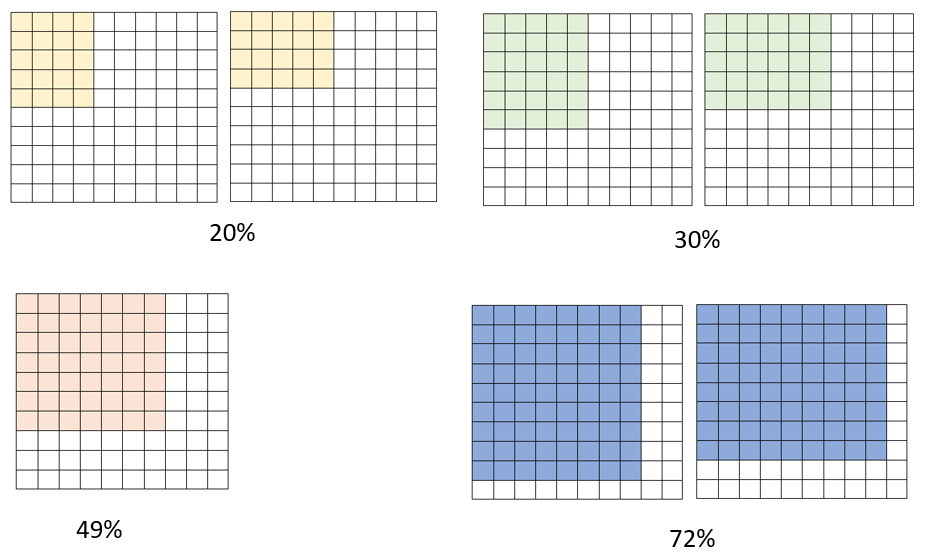
Nimm dir ein Blatt Papier und einen Stift. Übertrage die folgenden Prozentangaben auf dein Blatt und zeichne dazu die passenden Hunderterfelder.
- 20%
- 30%
- 49%
- 72%
2. Prozentstreifen
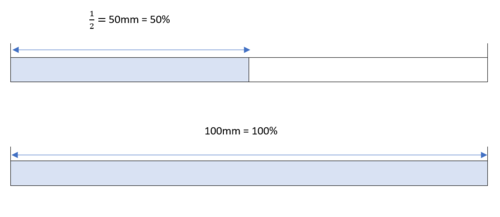
Der Prozentstreifen wird durch einen Balken dargestellt. Der gesamte Balken entspricht 100%. Um Prozentwerte einfach darstellen zu können, wählt man als Länge des Balkens 100mm = 10cm. Also gilt:
100mm = 100%
1mm = 1%
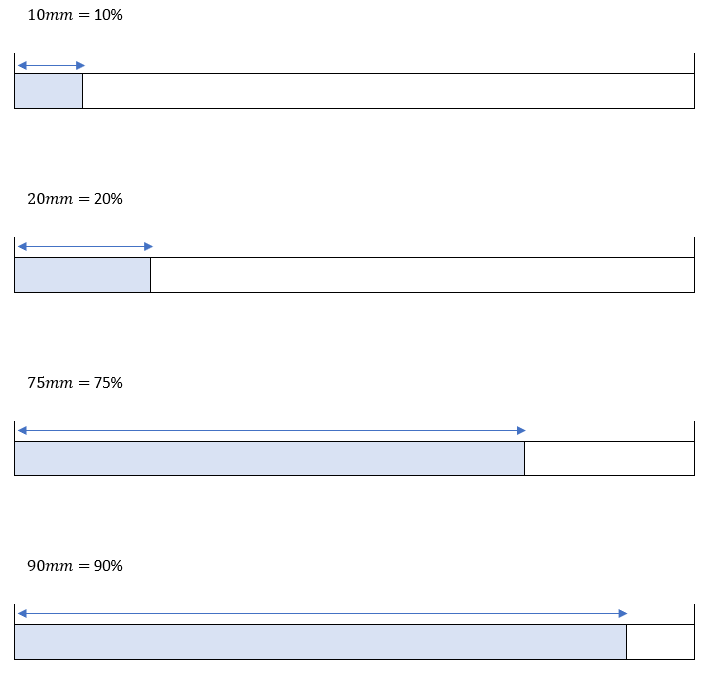
Nimm dir ein Blatt Papier und einen Stift. Übertrage die folgenden Prozentangaben auf dein Blatt und zeichne dazu die passenden Prozentstreifen.
- 10%
- 20%
- 75%
- 90%
3. Prozentkreis
Beim Prozentkreis wird das Ganze als eine volle Kreisfläche dargestellt.
100% entsprechen also 360°.
Für einen kleineren Prozentsatz zeichnet man einen Kreissektor. Dafür muss der Winkel entsprechend dem dazugehörigen Prozentsatz berechnet werden. Wenn 100% also 360° entsprechen, dann entspricht 1% genau 3,6°.
| Prozentsatz | Winkel des Kreissektors |  |
|---|---|---|
| 5% | 18()
| |
10%()
|
36° | |
| 25% | 90°()
| |
| 40% | 144°()
| |
50%()
|
180° | |
| 75% | 270°()
|